问题简介
SAT问题(Boolean Satisfiability Problem)是判断一个以合取范式形式给出的逻辑命题公式是否存在一个真值指派,使得公式为真。
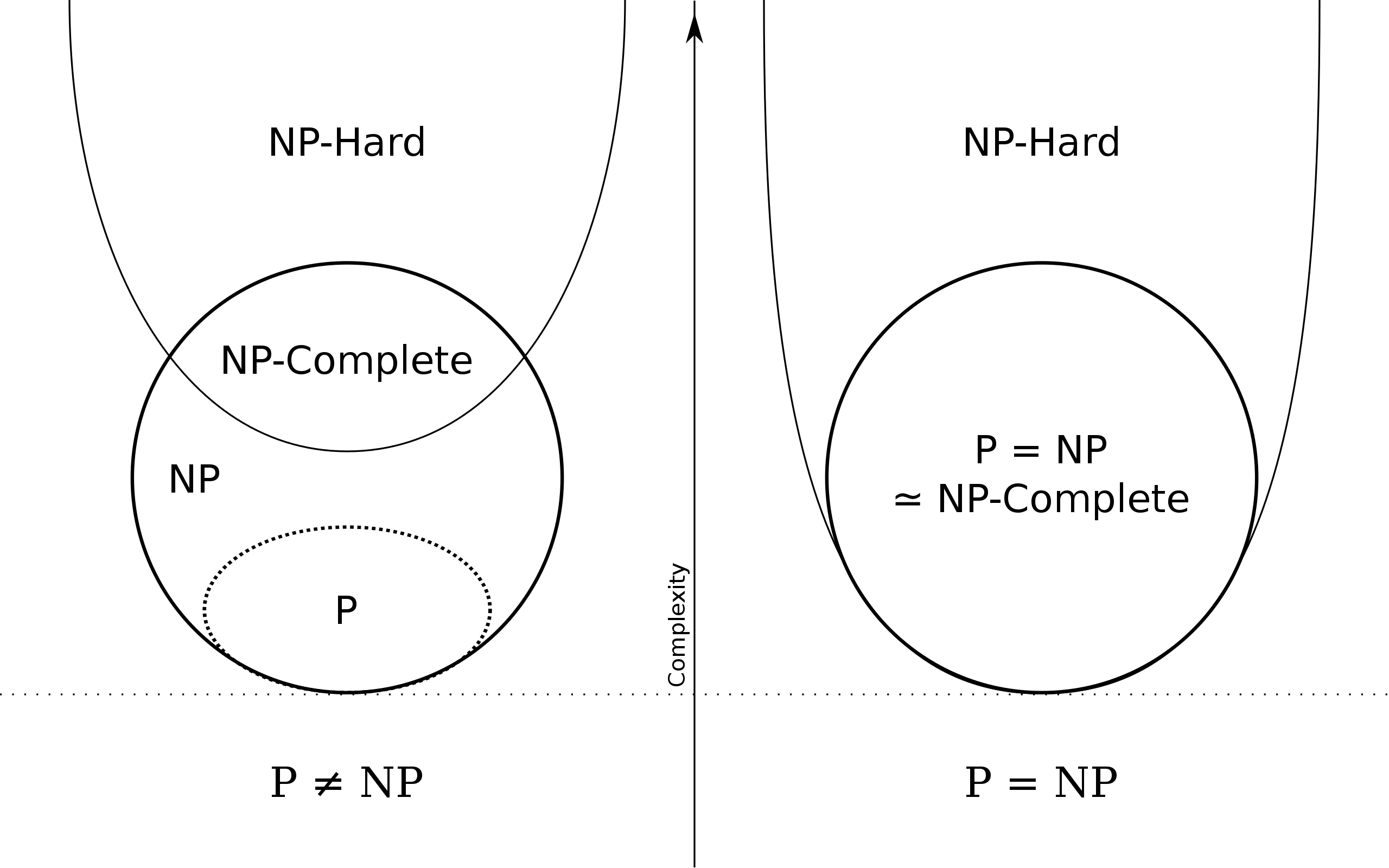
SAT 可满足问题是第一个被证明的NP问题(就是能在多项式时间验证答案正确与否的问题)
解决方法:
- 完备方法:枚举法、贪婪算法、局部搜索法等
- 不完备方法:各类启发式算法,如演化算法、退火算法、蚁群算法等
P问题:在多项式时间内能够求解,是一类可以通过确定性图灵机在多项式时间(Polynomial time)内解决的问题集合。
NP问题:在多项式时间里能够验证是否有解,可以通过非确定性图灵机(Non-deterministic Turing Machine)在多项式时间(Polynomial time)内解决的决策问题集合。
NOTE:P是NP的子集,也就是说任何可以被图灵机在多项式时间内解决的问题都可以被非确定性的图灵机解决。
如果一个决策问题 L 是 NP-complete的,那么L具备以下两个性质:
- L 是 NP(给定一个解决NP-complete的方案(solution,感兴趣的读者可以思考一下solution 和 answer的区别),可以很快验证是否可行,但不存在已知高效的方案 。)
- NP里的任何问题可以在多项式时间内转为 L。
而NP-hard只需要具备NP-complete的第二个性质,因此NP-complete是NP-hard的子集。
求解方法
研究中遇到的大部分问题都是NPC问题,选择的方法可以视问题的输入规模而定:
- 规模小:搜索法,利用搜索策略在指数时间内求解问题
- 规模大:随机算法,在多项式时间内“高概率”地精确求解问题;近似算法,也可以考虑在多项式时间内求得问题的一个近似解
reference:
https://www.cnblogs.com/sancyun/p/4250360.html
https://baike.baidu.com/item/布尔可满足性问题/4715567?fr=aladdin
https://blog.csdn.net/zhushiq1234/article/details/79484280
https://en.wikipedia.org/wiki/NP_(complexity)