向量表示

量子计算的基本单位是量子比特，量子比特用向量 $|\psi\rangle$ (狄拉克Dirac符号)来描述。

基态: $|g\rangle=|1\rangle=\left[ \begin{matrix} 0 \\ 1 \end{matrix} \right]$

激发态: $∣e\rangle=|0\rangle=\left[ \begin{matrix} 1 \\ 0 \end{matrix} \right]$

在量子理论中，描述量子态的向量称为态矢，态矢分为左矢和右矢。相同描述对象的左矢和右矢互为转置共轭。

pyqpanda中，dagger()函数可用于对逻辑门进行转置共轭操作

右失（ket）： $|\psi\rangle=\left[ \begin{matrix} c_1 & c_2 & \cdots & c_n \end{matrix} \right]^T=\left[ \begin{matrix} c_1 \\ c_2 \\ \vdots \\ c_n \end{matrix} \right]$

左失（bra）： $\langle\psi|=\left[ \begin{matrix} c_1^* & c_2^* & \cdots & c_n^* \end{matrix} \right]$

并不是任意的二维向量都能用来描述一个qubit的状态，描述量子态的向量的模长必须为1，所谓向量的模长定义如下：

$M(\alpha) = \sqrt{|a_{1}|^{2} + |a_{2}|^{2} + … + |a_{n}|^{2}}$

量子比特各维度的平方为量子处于该状态的概率。

向量计算

基

对于一组向量 $|u_1\rangle, |u_2\rangle, \cdots, |u_n\rangle$ 张成（spanning）的 $n$ 维空间 $C^n$ ，空间中的任意向量可以表示为： $|v\rangle=\sum_i x_i u_i$ ,这个集合 ${|u_1\rangle, |u_2\rangle, \cdots, |u_n\rangle}$ 就称为 $C^n$ 的基（basis）。

内积

在 $C^n$ 上的内积表示为（注意 $a_i^*$ 为 $a_i$ 的共轭！）：

$\langle \alpha | \beta \rangle = (|\alpha\rangle, |\beta\rangle) = ((a_1, \cdots ,a_n),(b_1, \cdots, b_n)) = \sum_{i=1}^{n}a_i^*b_i$

可以看做 $\langle \alpha|$ 共轭转置后得到的 $1 \times n$ 的矩阵与 $| \beta \rangle$ 构成的 $n \times 1$ 的矩阵的积,内积的结果是一个值。

外积

外积 $| \alpha \rangle \langle \beta |$ 可以看做 $\langle \alpha|$ 的 $n \times 1$ 的矩阵与 $| \beta \rangle$ 共轭转置后构成的 $1 \times n$ 的矩阵的积,外积的结果是一个矩阵！

张量积

向量 $|\alpha\rangle$ 、 $|\beta\rangle$ 在 $C^n$ 、 $C^m$ 中的张量积为 $C^{n\times m}$ 中的向量： $|\alpha\rangle\otimes|\beta\rangle=|\alpha\rangle|\beta\rangle=|\alpha\beta\rangle$ ，计算方法为：

$\left[ \begin{matrix} a_1 \\ a_2 \end{matrix} \right]\times\left[ \begin{matrix} b_1 \\ b_2 \end{matrix} \right] = \left[ \begin{matrix} a_1 b_1 \\ a_1 b_2 \\ a_2 b_1 \\ a_2 b_2 \end{matrix} \right]$

常用算子（常见量子逻辑门）矩阵形式

单比特量子逻辑门

当单比特量子逻辑门作用于量子比特时，为门在前比特在后进行矩阵相乘，进而改变比特状态。

其中:

$I$ 门不改变比特状态
$Hadamard$ 门可以使量子比特进入混沌态，即激发与否的概率均为一半
$Pauli-X$ 会使量子状态翻转
量子的状态改变通常通过旋转实现

多比特量子逻辑门

当多比特量子逻辑门作用于多个量子比特时，为门在前，多个量子比特的张量积在后，进行矩阵相乘。

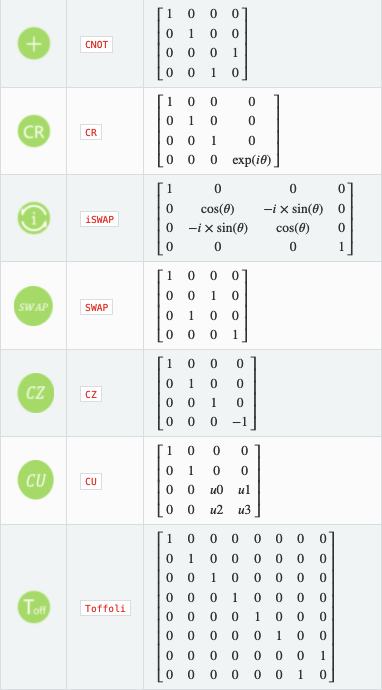
量子线路图

基本约定

在关系图中，每条实线都描述一个量子比特，更常见地是描述一个量子比特寄存器。按照约定，最上面那根线是量子比特寄存器0，其余的按顺序标记。根据描述，上面的示例线路作用于两个量子比特（或等效为作用于两个寄存器，每个寄存器由一个量子比特组成）。作用于一个或多个量子比特寄存器的门用一个框表示。例如，符号

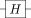
量子门按时间顺序排列，最左侧的门是应用于量子比特的第一个门。也就是说，如果你将线描述为包含量子态，那么这些线将按图中从左到右的顺序带着量子态通过每个门。也就是说

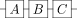
是酉矩阵 $CBA$ 。矩阵乘法遵守相反的约定，即最先应用最右侧的矩阵。不过，在量子线路图中，最先应用的是最左侧的门。这种差异有时可能会导致混淆，因此有必要记下线性代数表示法和量子关系图之间的这一明显差异。

受控门

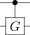
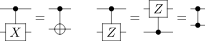
在这里，黑色圆圈表示门受控的量子位，垂直线表示当控制量子比特采用值1时应用的酉操作。对于 $G=X$ 和 $G=Z$ 的特殊情况，我们引入了以下表示法来描述门的受控版本（请注意，受控 $X$ 门是 $CNOT$ 门）：

测量运算符

在线路图中直观呈现的剩余操作是测量。测量采用量子比特寄存器、对其进行测量，然后以经典信息的形式输出结果。测量操作由计量符号表示，它始终将输入看做是一个量子比特寄存器（表示为实线），将输出看做是经典信息（表示为双线）。具体来说，这种子线路如下所示：

References:
https://blog.csdn.net/si_ying/article/details/108303988
https://pyqpanda-toturial.readthedocs.io/
https://docs.microsoft.com/zh-cn/azure/quantum/concepts-circuits
https://www.cxyzjd.com/article/qq_43391414/118766778
https://swardsman.github.io/learning-q-sharp/

C_Meng PSNA

量子计算学习笔记