C_Meng PSNA

Never wait for the storm to pass, just dance in the rain.

0%

Posted on Valine:

本文提炼自：https://zhuanlan.zhihu.com/p/35642367

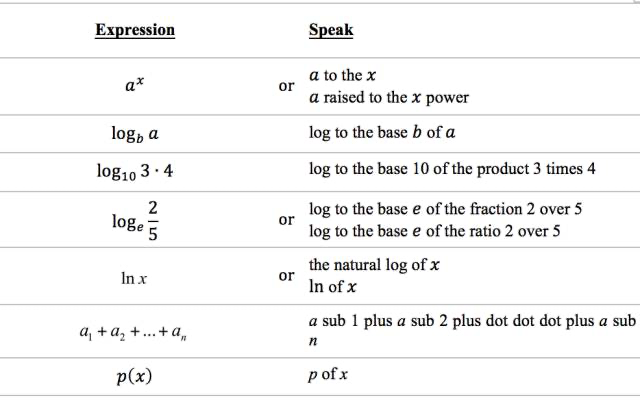
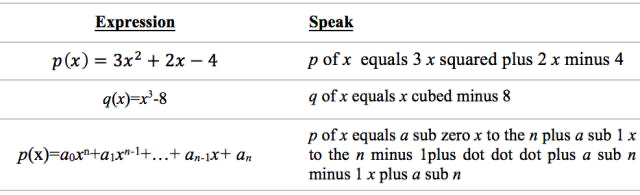
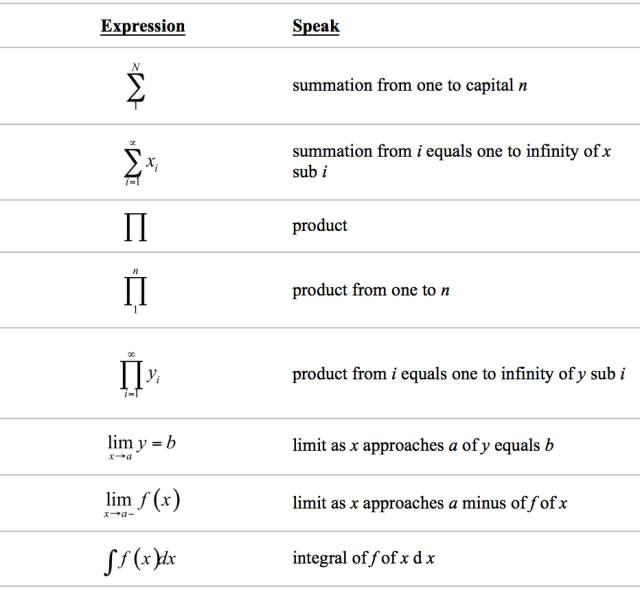
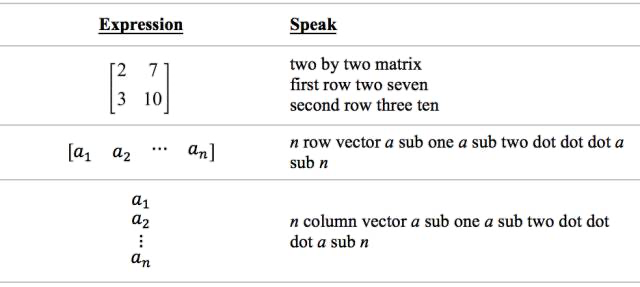
冠词是置于名词前并限定名词的意义的虚词，分为定冠词和不定冠词，实际使用中，还会出现零冠词，共三种情况。

定冠词：THE

用于表示特指。

一般用法：

  1. 表示特指：特指某(些)人或某(些)物(包括用于上文提到过的人或物之前，以及说话双方都知道的人或物)。如：We have a cat and two dogs. The cat is black and the dogs are white. 我们养了一只猫和两只狗，猫是黑的，狗是白的。
  2. 表示独一无二：用在世界上“独一无二”的事物的名词前。如：The earth goes round the sun. 地球绕着太阳转。
  3. 用于最高级前：即用于形容词或副词的最高级前。如：Who picked the most apples? 谁摘的苹果最多?
  4. 用于序数词或方位词之前。如：He was the first man to think of it. 他是第一个想到这一点的人。
  5. 用于乐器名词前：表示相应乐器的演奏。如：Besides the violin, he plays the piano and the flute. 除了拉提琴，他还能弹钢琴和吹笛子。
  6. 表示人体部位：用于某些介词短语中指身体的某个部位。如：He patted me on the back. 他拍了拍我的背。
  7. 用于表示一家人：用于在姓氏的复数形式之前表示一家人或夫妇二人。如：The Smiths live in the apartment above ours. 史密斯一家住在我们楼上的一套住房里。
  8. 用于江河湖海等前：用于江河湖海、山脉群岛、海湾海峡等地理名词前。如：The Yellow River flows into the Yellow Sea. 黄河流人黄海。
  9. 用于某些含有普通名词的专有名词前：用于某些国名、组织机构、建筑物、报纸杂志、会议条约等含有普通名词与其他词构成的专有名词。如：We visited the Great Wall yesterday. 我们昨天去参观了长城。

其他用法：

  1. 用于整十的复数数词前：表示几十年代。如：This happened in the seventies. 这发生在七十年代。
  2. 用于比较级前：用于“the+比较级，the+比较级”结构中表示“越……就越……”。如：The sooner we operate now the safer. 越早动手术越安全。
  3. 用于表示类别：用于“the+某些形容词或过去分词”中表示一类人。如：Do you think the rich should pay more taxes to help the poor? 你认为富人是否应当多交点税来帮助穷人?
  4. 用于国籍名词前表总称：用于“the+某些国籍的形容词”中表示某国人的总称。如：The French are famous for their food. 法国人因法国菜而出名。
  5. 用于集合名词前表总称：用于“the + police / public等集合名词”中表示这类人的总称。如：The police are looking for the murderer. 警察正在寻找那个凶手。
  6. 用于修饰same, only, very等形容词：即用于“the same / only / very +名词”结构中。如：That’s the only reason. 那是唯一的理由。
  7. 用于单位名词前表标标准：即用于“单位词”（hour, day, month, year, dozen, gallon, ton, yard等）前表示标准，相当于汉语的“按”“论”“每”等。如：They let out cars by the day. 他们按天出租汽车。

但是，by weight（按重量）习惯上不用冠词。如：Bananas are usually sold by weight. 香蕉通常按重量卖。

不定冠词：A、AN

用于表示泛指。

一般用法

  1. 表类别：即指人或事物的类别。如：A teacher is a person who teaches. 教师就是教书的人。
  2. 表数量：即表示数量“一”。如：I’ll be able to finish it in a day or two. 在一两天内我会完成此事。
  3. 表同一性：即表示“同一”，说明事物的同一性质、特征、大小或程度等。如：This hat and that one are of a shape. 这顶帽子和那顶一样大。
  4. 表程度：用于most前表示“非常”“十分”。如：It’s a most boring book. 这是一本非常枯燥乏味的书。

其他用法

  1. 用于序数词前：用在序数词前表示“再一”“又一”。如：She thanked him a second time. 她再次向他道谢。
  2. 用于由动词转化来的名词前：表示一次、一番等义(通常与 have, take, make, give 等动词连用)。如：We’ve already had a try at it. 我们已经试过一下。
  3. 用于专有名词前：相当于a certain，意为“一个”“某个”。如：The house next door has been bought by a Mr Jones. 隔壁的 房子被一个叫琼斯的先生的人买下了。
  4. 用于抽象名词前：使之具体化，表示与该之相关的具体的人或事。如：He was a success in business. 他事业成功。

零冠词

用于表示泛指。

  1. 表泛指的不可数名词或复数名词前。如：Snow was failing. 正在下雪。
  2. 倒装的让步状语从句中：在as(虽然)引导让步状语从句前面的单数可数名词前不用冠词。如：Child as he was, he knew how to help others. 他虽是个孩子，但已知识如何帮助别人。
  3. 某些特殊词前：例如在man(人，人类), word(消息)的前面不用冠词。如：Man is a rational animal. 人是理性的动物。
  4. 又如动词 turn(变成)，go(变成)后作表语的名词前通常用不用冠词。如：He was a teacher before he turned writer. 他在成为作家之前是教师。
  5. 独立主格结构中：在表示伴随或补充说明用用的独立主格结构中，名词前不用冠词。如：The teacher came in, book in hand. 老师走进教室，手里拿着书。
  6. “(a) kind [sort] of＋名词”结构的“名词”前：该结构中的“名词”不管是单数还是复数，其前都通常用零冠词。如：This kind of book is very interesting. 这种书很有趣。
  7. 表抽象意义的单数名词前：当单数可数名词含义抽象化具有形容词意味时，通常用零冠词。如：I was fool enough to accept his offer. 我接受他的提议真是太傻了。

Posted on In Valine:

泡利算符类

泡利算符是一组三个2×2的幺正厄米复矩阵，又称酉矩阵。我们一般都以希腊字母 $\sigma$ 来表示。 在 QPanda 中我们称它们为X门，Y门，Z门。它们对应的矩阵形式如下。

X:
$\sigma_x = \left[\begin{matrix}
0 & 1 \\
1 & 0
\end{matrix}\right]$

Y:
$\sigma_y = \left[\begin{matrix}
0 & -i \\
i & 0
\end{matrix}\right]$

Z:
$\sigma_z = \left[\begin{matrix}
1 & 0 \\
0 & -1
\end{matrix}\right]$

每个抛离矩阵有两个特征值，+1和-1，其对应的归一化特征向量为：

$\psi_{x+}=\frac{1}{\sqrt{2}}\left[\begin{matrix}
1 \\
1
\end{matrix}\right]$

$\psi_{x-}=\frac{1}{\sqrt{2}}\left[\begin{matrix}
1 \\
-1
\end{matrix}\right]$

$\psi_{y+}=\frac{1}{\sqrt{2}}\left[\begin{matrix}
1 \\
i
\end{matrix}\right]$

$\psi_{y-}=\frac{1}{\sqrt{2}}\left[\begin{matrix}
1 \\
-i
\end{matrix}\right]$

$\psi_{z+}=\left[\begin{matrix}
1 \\
0
\end{matrix}\right]$

$\psi_{z-}=\left[\begin{matrix}
0 \\
1
\end{matrix}\right]$

泡利算符的运算规则

  1. 泡利算符与自身相乘得到是单位矩阵
  2. 泡利算符与单位矩阵相乘，无论是左乘还是右乘，其值不变
  3. 顺序相乘的两个泡利算符跟未参与计算的泡利算符是i倍的关系
  4. 逆序相乘的两个泡利算符跟未参与计算的泡利算符是−i倍的关系

接口介绍

1
2
3
4
5
6
7
8
9
10
11
12
13
14
from pyqpanda import *

if __name__=="__main__":
    # 构造一个空的泡利算符类
    p1 = PauliOperator()

    # 2倍的"泡利Z0"张乘"泡利Z1"
    p2 = PauliOperator("Z0 Z1", 2)

    # 2倍的"泡利Z0"张乘"泡利Z1" + 3倍的"泡利X1"张乘"泡利Y2"
    p3 = PauliOperator({"Z0 Z1": 2, "X1 Y2": 3})

    # 构造一个单位矩阵，其系数为2，等价于p4 = PauliOperator("", 2)
    p4 = PauliOperator(2)

其中PauliOperator p2(“Z0 Z1”, 2)表示的是 $2\sigma_{0}^{z} \otimes \sigma_{1}^{z}$ ,这里的 $\otimes$ 表示克罗内克积（Kronecker product），也称作张量积、张乘。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
from pyqpanda import *

if __name__=="__main__":

    a = PauliOperator("Z0 Z1", 2)
    b = PauliOperator("X5 Y6", 3)

    plus = a + b
    minus = a - b
    muliply = a * b

    print("a + b = ", plus)
    print("a - b = ", minus)
    print("a * b = ", muliply)

    print("Index : ", muliply.getMaxIndex())

    index_map = {}
    remap_pauli = muliply.remapQubitIndex(index_map)

    print("remap_pauli : ", remap_pauli)
    print("Index : ", remap_pauli.getMaxIndex())

reference:
https://pyqpanda-toturial.readthedocs.io/zh/latest/PauliOperator.html
https://www.bilibili.com/video/BV124411b7bd?p=3

Posted on Edited on In Valine:

最优化问题分为连续性的和离散性的。其中离散性的最优化问题又被称为组合最优化问题。

数学表达

$$\begin{split}
\min& f(x) &\leftarrow 目标函数 \\
s.t.& g(x) \geq 0 &\leftarrow 约束条件 \\
& x \in D &\leftarrow 定义域
\end{split}$$

常用求解方法

  1. 各种规划方法（线性，非线性）
  2. 蚁群算法
  3. 遗传算法
  4. 退火算法
  5. 粒子群算法
  6. 神经网络
  7. 搜索算法
  8. 拉格朗日松弛算法
  9. 近似算法
  10. 等

Posted on In Valine:

问题简介

SAT问题（Boolean Satisfiability Problem）是判断一个以合取范式形式给出的逻辑命题公式是否存在一个真值指派，使得公式为真。
SAT 可满足问题是第一个被证明的NP问题（就是能在多项式时间验证答案正确与否的问题）

解决方法：

  1. 完备方法：枚举法、贪婪算法、局部搜索法等
  2. 不完备方法：各类启发式算法，如演化算法、退火算法、蚁群算法等

P问题：在多项式时间内能够求解，是一类可以通过确定性图灵机在多项式时间(Polynomial time)内解决的问题集合。

NP问题：在多项式时间里能够验证是否有解，可以通过非确定性图灵机(Non-deterministic Turing Machine)在多项式时间(Polynomial time)内解决的决策问题集合。

NOTE：P是NP的子集，也就是说任何可以被图灵机在多项式时间内解决的问题都可以被非确定性的图灵机解决。

如果一个决策问题 L 是 NP-complete的，那么L具备以下两个性质：

  1. L 是 NP（给定一个解决NP-complete的方案(solution，感兴趣的读者可以思考一下solution 和 answer的区别)，可以很快验证是否可行，但不存在已知高效的方案 。）
  2. NP里的任何问题可以在多项式时间内转为 L。

而NP-hard只需要具备NP-complete的第二个性质，因此NP-complete是NP-hard的子集。

求解方法

研究中遇到的大部分问题都是NPC问题，选择的方法可以视问题的输入规模而定：

  1. 规模小：搜索法，利用搜索策略在指数时间内求解问题
  2. 规模大：随机算法，在多项式时间内“高概率”地精确求解问题；近似算法，也可以考虑在多项式时间内求得问题的一个近似解

reference:
https://www.cnblogs.com/sancyun/p/4250360.html
https://baike.baidu.com/item/布尔可满足性问题/4715567?fr=aladdin
https://blog.csdn.net/zhushiq1234/article/details/79484280
https://en.wikipedia.org/wiki/NP_(complexity)

Posted on In Valine:

金字塔原理：

自下而上的思考，自上而下的表达。

  1. 文章结构中任一层次上的思想必须是其下一层次思想的概括
  2. 每一层次的思想要归属于同一范畴
  3. 每一层次的思想要按逻辑顺序组织

表达的逻辑

框架的构架

在较高层次的主题之间尽量用归纳法进行论述，在低层次用演绎方式论述。

  • 演绎推理：背景(情境)—冲突—问题—解决方案
  • 归纳推理：找到一组具体共同思想的名词，识别并剔除该组思想中与其他思想不相称的观点

深入的过程

通过纵向的思想引出主题和子主题之前的纵向关系。

“思想”定义：向读者发出新信息并引发读者疑问的语句。

纵向的思想实质是“疑问/回答”形式，这样更能吸引读者注意力。

序言的结构

以“情境、冲突、疑问、回答”方式来开篇，情境和冲突是读者熟知的事实。通过明确读者最初关心的问题，让后续的内容能吸引读者注意力。

  • 标准式： 情境—冲突—解决方案
  • 开门见山： 解决方案—情境—冲突
  • 突出忧虑： 冲突—情境—解决方案
  • 突出信心： 疑问—情境—冲突—解决方案

思考的逻辑（内容的填充）

  1. 应用时间顺序、结构顺序、重要程度顺序来构建思考逻辑树
  2. 总结句避免使用“缺乏思想”的句子，要说明行动产生的结果或目标
  3. 找出各结论之间的共性，得出金字塔尖的结论

四种主要的逻辑顺序：

  • 演绎顺序：大前提、小前提、结论—按照演绎推理组织的思想
  • 时间顺序：第一、第二、第三—按因果关系组织的思想
  • 结构顺序：将整体分割为部分进行评论，划分后的各部分需要符合以下要求：MECE
    • 各部分之间相互独立（mutually exclusive）
    • 所有部分完全穷尽（collectively exhaustive）
  • 重要性顺序：最重要、次重要，等等—按类别组织思想

解决问题的逻辑

界定问题：

  • 界定问题的框架
  • 展开问题的各要素
  • 发掘读者的疑问
  • 回答疑问

结构化分析问题：

  • 设计诊断框架
  • 收集信息
  • 建立逻辑树（回答是否问题）
  • 寻找解决方案

经典:建立诊断框架和逻辑树的指导来分析和引导思维，不仅能提高解决问题的效率，而且还简化了把结果构建成金字塔的工作。无目的的收集资料，会造成60%的无用功！！！

设计诊断框架的方法：其本身呈现有行结构/根据因果关系分解构建/归类分组

Reference:
https://www.jianshu.com/p/bdbf71572911
https://book.douban.com/review/7121761/
https://zhuanlan.zhihu.com/p/78548168

Posted on Edited on In Valine:

Pearson

要理解Pearson相关系数，首先要理解协方差（Covariance），协方差是一个反映两个随机变量相关程度的指标，如果一个变量跟随着另一个变量同时变大或者变小，那么这两个变量的协方差就是正值，反之相反，公式如下：

$$
\operatorname{cov}(x, y)=\frac{\sum_{i=1}^{n}\left(x_{i}-x_{\mu}\right)\left(y_{i}-y_{\mu}\right)}{n-1}
$$

虽然协方差能反映两个随机变量的相关程度（协方差大于0的时候表示两者正相关，小于0的时候表示两者负相关），但是协方差值的大小并不能很好地度量两个随机变量的关联程度。

为了更好的度量两个随机变量的相关程度，引入了Pearson相关系数，其在协方差的基础上除以了两个随机变量的标准：

$$
\delta^{2}=\frac{\sum_{i=1}^{n}\left(x_{i}-x_{\mu}\right)}{n}
$$

容易得出，pearson是一个介于-1和1之间的值，当两个变量的线性关系增强时，相关系数趋于1或-1；当一个变量增大，另一个变量也增大时，表明它们之间是正相关的，相关系数大于0；如果一个变量增大，另一个变量却减小，表明它们之间是负相关的，相关系数小于0；如果相关系数等于0，表明它们之间不存在线性相关关系。

$$
p_{x, y}=\operatorname{cor}(x, y)=\frac{\operatorname{cov}(x, y)}{\delta x \delta y}=\frac{E\left[\left(x-x_{\mu}\right)\left(y-y_{\mu}\right)\right]}{\delta x \delta y}
$$

Spearman

斯皮尔曼相关性系数，通常也叫斯皮尔曼秩相关系数。“秩”，可以理解成就是一种顺序或者排序，那么它就是根据原始数据的排序位置进行求解，这种表征形式就没有了求皮尔森相关性系数时那些限制。下面来看一下它的计算公式：

$$
\rho_{s}=1-\frac{6 \sum d_{i}^{2}}{n\left(n^{2}-1\right)}
$$

计算过程就是：
对两个变量（X，Y）的数据进行排序（统一用升序或降序），每个变量在排序之后的位置即为其秩次（X’, Y’），原始位置相同的X，Y的秩次X’, Y’的差值即为 $d_i$ 。n是变量的个数（或者对数）。

Kendall

Kendall相关系数是对于定类变量的统计，之前讲pearson是对定距变量的统计，而spearman是对定序变量的统计。

Kendall相关系数的计算公式：

$$
Kendall1=\frac{C-D}{\frac{1}{2} N\left(N-1\right)}
$$

另一个计算公式：

$$
Kendall2=\frac{C-D}{\sqrt{\left(N_{3}-N_{1}\right)\left(N_{3}-N_{2}\right)}}
$$

其中C表示的是两变量中一致性元素的对数，D是不一致性元素的对数。
举例来讲，如果要计算相关性的数据是一个nx2的矩阵M，那么如果 $m_{i,1}$ > $m_{j,1}$ 且 $m_{i,2} > m_{j,2}$，或 $m_{i,1} < m_{j,1}$ 且 $m_{i,2} < m_{j,2}$ ，则称 $m_i$ 和 $m_j$ 构成一个一致性元素对。反之则为不一致性元素对。

第一个和第二个公式的区别在于，当两变量任何一个中都不存在相同元素时用公式1，两变量中任何一个中存在相同元素用2。

其中N为样本数量。再说N3，N2，N1。

$$
\mathrm{N} 3=\frac{1}{2} N(N-1)
$$

N2、N1就比较复杂，它们各指向一个变量，但是计算方法一致：

$$
\mathrm{N} 2=\sum_{i=1}^{s} \frac{1}{2} v_{i}\left(v_{j}-1\right)
$$

s是指该变量中拥有相同元素的小集合的个数，v就是每个集合中元素的个数。

Reference:
https://blog.csdn.net/ichuzhen/article/details/79535226
https://blog.csdn.net/zmqsdu9001/article/details/82840332?utm_medium=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-1.edu_weight&depth_1-utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-1.edu_weight
https://www.jianshu.com/p/93fd5ab408ae