写给自己:
- 不管别人有没有催,不管有没有投稿日,都要给自己一个deadline
- 想法不成熟也没关系,方法有瑕疵也没关系,总之先开始写,把想到的东西都写下来
- 整理出第一版,就算再烂,也比没有强
- 拿着写好内容,再去找各路大神讨论,不断优化,事半功倍
写给自己:
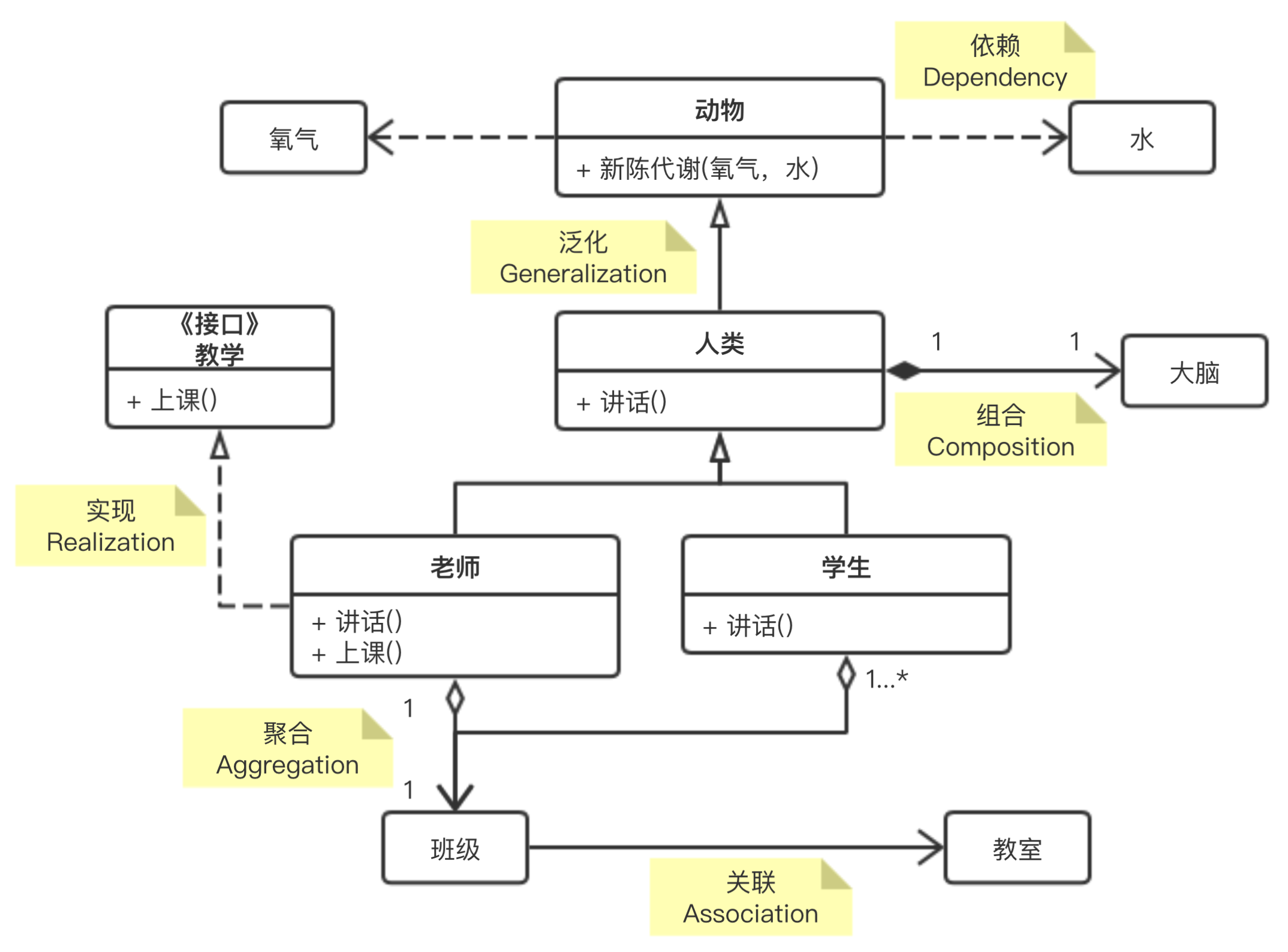
| 关系名称 | 说明 | 图形 |
|---|---|---|
| 泛化(Generalization) | 是一种继承关系, 表示一般与特殊的关系, 它指定了子类如何特化父类的所有特征和行为. | 带三角箭头的实线,箭头指向父类 |
| 实现(Realization) | 是一种类与接口的关系, 表示类是接口所有特征和行为的实现. | 带三角箭头的虚线,箭头指向接口 |
| 关联(Association) | 是一种拥有的关系, 它使一个类知道另一个类的属性和方法 | 带普通箭头(或实心三角形箭头)的实心线,指向被拥有者 |
| 聚合(Aggregation) | 是整体与部分的关系, 且部分可以离开整体而单独存在 | 带空心菱形的实心线,菱形指向整体 |
| 组合(Composition) | 是整体与部分的关系, 但部分不能离开整体而单独存在 | 带实心菱形的实线,菱形指向整体 |
| 依赖(Dependency) | 是一种使用的关系, 即一个类的实现需要另一个类的协助 | 带箭头的虚线,指向被使用者 |
多目标优化是多准则决策的一个领域,它是涉及多个目标函数同时优化的数学问题。多目标优化已经应用于许多科学领域,包括工程、经济和物流,其中需要在两个或多个相互冲突的目标之间进行权衡的情况下作出最优决策。分别涉及两个和三个目标的多目标优化问题的例子有:在购买汽车时降低成本,同时使舒适性最大化;在使车辆的燃料消耗和污染物排放最小化的同时将性能最大化。在实际问题中,甚至可以有三多个目标。
对于非平凡多目标优化问题,不存在同时优化每个目标的单个解决方案。在这种情况下,目标函数被说成是冲突的,并且存在一个(可能无限)数量的帕累托最优解。如果目标函数在值上不能改进而不降低其他一些目标值,则解决方案称为非支配、Pareto最优、Pareto有效或非劣解。如果没有额外的主观偏好信息,所有Pareto最优解都被认为是同样好的(因为向量不能完全排序)。研究人员从不同的角度研究多目标优化问题,从而在设置和解决多目标优化问题时存在不同的求解哲学和目标。目标可以是找到帕累托最优解的代表性集合,and/or量化满足不同目标的折衷,and/or找到满足人类决策者decision maker(DM)的主观偏好的单一解决方案。
$$
\begin{array}{cl}{\min / \max } & {f_{m}(x), \quad m=1,2, \ldots, M} \\ {\text { subject to }} & {g_{j}(x) \geq 0, \quad j=1,2, \ldots, J} \\ {} & {h_{k}(x)=0, \quad k=1,2, \ldots, K} \\ {} & {x_{i}^{(Lower)} \leq x_{i} \leq x_{i}^{(Upper)}, \quad i=1,2, \ldots, n} \end{array}
$$
| 年份 | 事件 | 相关论文 |
|---|---|---|
| 1906 | Pareto提出核心思想 | Pareto, V. (1906). Manuale di economia politica (Vol. 13). Societa Editrice. |
| 1979 | Stadler, W. 对帕累托最优进一步回顾 | Stadler, W. (1979). A survey of multicriteria optimization or the vector maximum problem, part I: 1776–1960. Journal of Optimization Theory and Applications, 29(1), 1-52. |
| 2008 | Miettinen, K.提出一种混合方法解决多目标问题 | Miettinen, K., Ruiz, F., & Wierzbicki, A. P. (2008). Introduction to multiobjective optimization: interactive approaches. In Multiobjective Optimization (pp. 27-57). Springer, Berlin, Heidelberg. |
| 2014 | Deb, K.对多目标优化进行回顾 | Deb, K. (2014). Multi-objective optimization. In Search methodologies (pp. 403-449). Springer, Boston, MA. |
| 2018 | Sener, O., & Koltun, V.提出多任务学习来作为多目标优化的策略 | Sener, O., & Koltun, V. (2018). Multi-task learning as multi-objective optimization. In Advances in Neural Information Processing Systems (pp. 524-535). |
多目标优化算法归结起来有传统优化算法和智能优化算法两大类。
从九十年代初开始,进化算法系列算法被统一,如遗传算法等。
在单目标优化问题中,通常最优解只有一个,而且能用比较简单和常用的数学方法求出其最优解。然而在多目标优化问题中,各个目标之间相互制约,可能使得一个目标性能的改善往往是以损失其它目标性能为代价,不可能存在一个使所有目标性能都达到最优的解,所以对于多目标优化问题,其解通常是一个非劣解的集合——Pareto解集。
帕累托最优(Pareto Optimal):帕雷托最优是指资源分配的一种理想状态。给定固有的一群人和可分配的资源,如果从一种分配状态到另一种状态的变化中,在没有使任何人境况变坏的前提下,使得至少一个人变得更好,这就是帕雷托改善。帕雷托最优的状态就是不可能再有更多的帕雷托改善的状态;换句话说,不可能在不使任何其他人受损的情况下再改善某些人的境况。帕累托最优解集的边界(boundary)被称为帕累托最优前沿面(Pareto-optimal front)。
在存在多个Pareto最优解的情况下,如果没有关于问题的更多的信息,那么很难选择哪个解更可取,因此所有的Pareto最优解都可以被认为是同等重要的。由此可知,对于多目标优化问题,最重要的任务是找到尽可能多的关于该优化问题的Pareto最优解。因而,在多目标优化中主要完成以下两个任务:
第一个任务是在任何优化工作中都必须的做到的,收敛不到接近真正Pareto最优解集的解是不可取的,只有当一组解收敛到接近真正Pareto最优解,才能确保该组解近似最优的这一特性。
线性加权法,其中权重代表了每个目标函数的重要程度。
$$
\begin{array}{rl}{\min } & {F(x)=\sum_{m=1}^{M} w_{m} f_{m}(x)} \\ {\text { subject to }} & {g_{j}(x) \geq 0, \quad j=1,2, \ldots, J} \\ {} & {h_{k}(x)=0, \quad k=1,2, \ldots, K} \\ {} & {x_{i}^{(Lower)} \leq x_{i} \leq x_{i}^{(Upper)}, \quad i=1,2, \ldots, n}\end{array}
$$
优点:简单
缺点:很难设定一个权重向量能够去获得帕累托最优解;在一些非凸情况不能够保证获得帕累托最优解
只保留一个目标函数,其他的目标函数被设定的值约束。
$$
\begin{array}{cl}{\min } & {f_{\mu}(x)} \\ {\text {subject to }} & {f_{m}(x) \leq \epsilon_{m}, \quad m=1,2, \ldots, M \text { and } m \neq \mu} \\ {} & {g_{j}(x) \geq 0, \quad j=1,2, \ldots, J} \\ {} & {h_{k}(x)=0,} \quad {k=1,2, \ldots, K} \\ {} & {x_{i}^{(Lower)} \leq x_{i} \leq x_{i}^{(Upper)},} \quad {i=1,2, \ldots, n}\end{array}
$$
优点:能够应用到凸函数和非凸函数场景下
缺点:函数需要精心选择;需要在独立目标函数的最小值或最大值之内
$$
\begin{array}{cl}{\min } & {l_{p}(x)=\left(\sum_{m=1}^{M} w_{m}\left|f_{m}(x)-z_{m}^{*}\right|\right)^{1 / p}} \\ {\text { subject to }} & {g_{j}(x) \geq 0, \quad j=1,2, \ldots, J} \\ {} & {h_{k}(x)=0, \quad k=1,2, \ldots, K} \\ {} & {x_{i}^{(Lower)} \leq x_{i} \leq x_{i}^{(Upper)}, \quad i=1,2, \ldots, n}\end{array}
$$
优点:weighted Techebycheff metirc能够保证获得所有帕累托最优解
缺点:需要有每个函数最大值和最小值的先验知识;需要每个目标函数的 $z^{*}$ 能够独立被找到;对于较小的p值,不一定保证所有能够获得所有帕累托最优解;随着p增加,问题会变得不可求导
基于遗传算法的多目标优化就是利用遗传算法的原理来搜索帕累托最优前沿面。
遗传算法相比与传统算法的优点是能够得到一个最优解集,而不是单单一个最优解,这样给我们更多的选择。但计算复杂度可能稍高,而且里面涉及的一些函数需要精心设计。
详见:https://imonce.github.io/2019/11/07/启发式算法学习(三):遗传算法/
多目标优化算法相对成熟,在不同的问题使用不同的优化算法。NSGA-II, SPEA 或者 MOPSO都是可选项,而到底选择哪一个方法,还需要根据特定的情景选择。
尽管多目标优化算法应用于动态的制造系统,dynamic manufacturing systems,但是制造系统和很复杂的,并且是动态的,因此算法还是有一定的缺陷性。
未来发展方向:
因为多种多目标方法已经被提出,混合方法 hybrid method可以被进一步发展。
现在的动态制造系统中的多目标优化算法需要动态调度的能力
Reference:
https://www.jiqizhixin.com/graph/technologies/cf8932be-519a-4fd9-84f9-c6ffa997a554
https://blog.csdn.net/paulfeng20171114/article/details/82454310
https://hpzhao.github.io/2018/09/17/多目标优化四种方法/
https://zh.wikipedia.org/wiki/帕累托最优
蚁群算法(Ant Colony Algorithm, AG, or Ant Colony Optimization, ACO),又称蚂蚁算法,是一种用来在图中寻找优化路径的机率型算法。它由Marco Dorigo于1992年在他的博士论文“Ant system: optimization by a colony of cooperating agents”中提出,其灵感来源于蚂蚁在寻找食物过程中发现路径的行为。蚁群算法是一种模拟进化算法,初步的研究表明该算法具有许多优良的性质。针对PID控制器参数优化设计问题,将蚁群算法设计的结果与遗传算法设计的结果进行了比较,数值仿真结果表明,蚁群算法具有一种新的模拟进化优化方法的有效性和应用价值。
蚂蚁会在其经过的路径上释放一种可以称之为“信息素”的物质,蚁群内的蚂蚁对“信息素”具有感知能力,它们会沿着“信息素”浓度较高路径行走,而每只路过的蚂蚁都会在路上留下“信息素”,这就形成一种类似正反馈的机制,这样经过一段时间后,整个蚁群就会沿着最短路径到达食物源了。可以分解为以下几步:
蚁群算法解决旅行商问题的流程:
这个利用TSP问题来说明这个数学模型,对于TSP问题,设蚂蚁群体中蚂蚁的数量为m,城市的数量为n,城市i与城市j之间的距离为 $d_{ij}$ ,t时刻城市i与城市j连接路径上的信息素浓度为 $c_{ij}(t)$ 。初始时刻,蚂蚁被放置在不同的城市里,且各城市键连接路径上的信息素浓度相同。然后蚂蚁将按一定概率选择线路,不放设 $p^k_{ij}(t)$ 为t时刻蚂蚁k从城市i转移到城市j的概率。“蚂蚁TSP”策略收到两方面的左右,首先是访问某城市的期望,领完便是其他蚂蚁释放的信息素浓度。所以已定义:
$$p_{ij}^{k}(t)=\left\lbrace\begin{array}{cll}
\frac{[c_{ij}(t)]^{a} * [n_{ij}(t)]^{b}}{\sum [c_{ij}(t)]^{a} * [n_{ij}(t)]^{b}} & , & j \in allowk \\
0 & , & j \notin allowk
\end{array}\right.$$
其中:
在蚂蚁遍历各城市的过程中,与实际情况相似的是,在蚂蚁释放信息素的同事,各个城市之间连接路径上的信息素的强度也在通过挥发等方式逐渐消失。为了描述这个特征,设ρ表示信息素挥发程度。这样所有蚂蚁完成走完一遍所有城市之后,各个城市键连接路径上的信息素浓度为
$$c_{ij}(t+1) = (1-\rho)*c_{ij}(t) + \Delta c_{ij}$$
$$\Delta c_{ij} = \sum \Delta c^k_{ij}$$
$\Delta c^k_{ij}$ 为第k只蚂蚁在城市i与城市j连接路径上释放信息素而增加的信息素浓度。
$\Delta c_{ij}$ 为所有蚂蚁在城市i与城市j连接路径上释放信息素而增加的信息素浓度。
一般情况下 $\Delta c^k_{ij}=\frac{Q}{L_k}$ ,若蚂蚁k从城市i访问了城市j,其中 $Q$ 为信息素常数, $L_k$ 为第k只蚂蚁经过路径总长度。
代码来源:https://blog.csdn.net/fanxin_i/article/details/80380733
1 | # -*- coding: utf-8 -*- |
Reference:
https://zh.wikipedia.org/wiki/蚁群算法
https://blog.csdn.net/fanxin_i/article/details/80380733
https://blog.csdn.net/qq_35109096/article/details/81126925
遗传算法(Genetic Alogrithm,GA)是最早由美国Holland教授提出的一种基于自然界的“适者生存,优胜劣汰”基本法则的智能搜索算法。该法则很好地诠释了生物进化的自然选择过程。遗传算法也是借鉴该基本法则,通过基于种群的思想,将问题的解通过编码的方式转化为种群中的个体,并让这些个体不断地通过选择、交叉和变异算子模拟生物的进化过程,然后利用“优胜劣汰”法则选择种群中适应性较强的个体构成子种群,然后让子种群重复类似的进化过程,直到找到问题的最优解或者到达一定的进化(运算)时间。
个体(染色体):自然界中一个个体(染色体)代表一个生物,在GA算法中,个体(染色体)代表了具体问题的一个解。
基因:在GA算法中,基因代表了具体问题解的一个决策变量,问题解和染色体中基因的对应关系如下所示
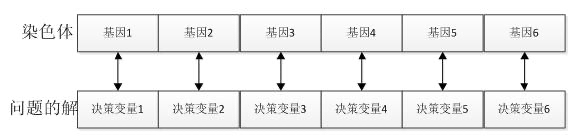
种群:多个个体即组成一个种群。GA算法中,一个问题的多组解即构成了问题的解的种群。
选择一种编码方案,然后在解空间内通过随机生成的方式初始化一定数量的个体构成GA的种群
种群的初始化和具体问题相关,一般来说可以采取某种分布(如高斯分布)在一定求解范围内随机获取
种群的评价即计算种群中个体的适应度值。假设种群population有popsize个个体。依次计算每个个体的适应度值及评价种群。或者利用启发式算法对种群中的个体(矩形件的排入顺序)生成排样图并依此计算个体的适应函数值(利用率),然后保存当前种群中的最优个体作为搜索到的最优解。
常见的选择操作有轮盘赌的方式:根据个体的适应度计算被选中的概率,公式如下:
$$P(x_j)=\frac{fit(x_j)}{\sum_{i=1}^n fit(x_i)}, j\in{1,2,…,n}$$
一般以概率阀值Pc控制是否进行单点交叉、多点交叉或者其他交叉方式生成新的交叉个体。
交叉操作也有许多种:单点交叉,两点交叉等。此处仅讲解一下两点交叉。首先利用选择操作从种群中选择两个父辈个体parent1和parent2,然后随机产生两个位置pos1和pos2,将这两个位置中间的基因位信息进行交换,便得到下图所示的off1和off2两个个体,但是这两个个体中一般会存在基因位信息冲突的现象(整数编码时),此时需要对off1和off2个体进行调整:off1中的冲突基因根据parent1中的基因调整为parent2中的相同位置处的基因。如off1中的“1”出现了两次,则第二处的“1”需要调整为parent1中“1”对应的parent2中的“4”,依次类推处理off1中的相冲突的基因。需要注意的是,调整off2,则需要参考parent2。
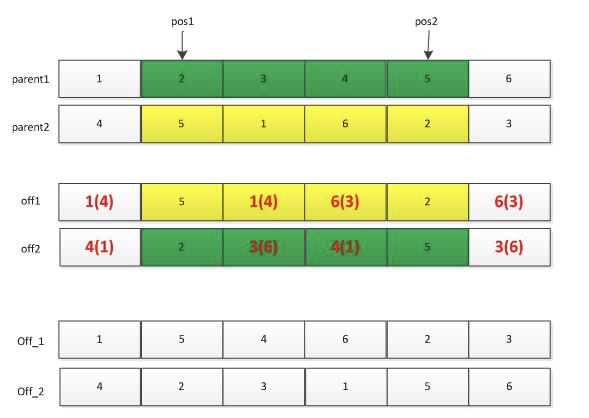
一般以概率阀值Pm控制是否对个体的部分基因执行单点变异或多点变异。
变异操作的话,根据不同的编码方式有不同的变异操作。
如果是浮点数编码,则变异可以就染色体中间的某一个基因位的信息进行变异(重新生成或者其他调整方案)。
如果是采用整数编码方案,则一般有多种变异方法:位置变异(调换同一个体的多个基因)和符号变异(正数变负数)。
求 $f(x,y)=21.5+x\times\sin(4\times\pi\times x) + y \times\sin(20\times\pi\times y)$ 的最大值
代码来自:
https://blog.csdn.net/qq_30666517/article/details/78637255
1 | # -*- coding:utf-8 -*- |
Reference:
https://blog.csdn.net/bible_reader/article/details/72782675
https://blog.csdn.net/qq_30666517/article/details/78637255
模拟退火算法(Simulated annealing algorithm,SAA)的思想借鉴于固体的退火原理,当固体的温度很高的时候,内能比较大,固体的内部粒子处于快速无序运动,当温度慢慢降低的过程中,固体的内能减小,粒子的慢慢趋于有序,最终,当固体处于常温时,内能达到最小,此时,粒子最为稳定。模拟退火算法便是基于这样的原理设计而成。
模拟退火算法从某一高温出发,在高温状态下计算初始解,然后以预设的邻域函数产生一个扰动量,从而得到新的状态,即模拟粒子的无序运动,比较新旧状态下的能量,即目标函数的解。如果新状态的能量小于旧状态,则状态发生转化;如果新状态的能量大于旧状态,则以一定的概率准则发生转化。当状态稳定后,便可以看作达到了当前状态的最优解,便可以开始降温,在下一个温度继续迭代,最终达到低温的稳定状态,便得到了模拟退火算法产生的结果。
状态空间也称为搜索空间,它由经过编码的可行解的集合所组成。而邻域函数应尽可能满足产生的候选解遍布全部状态空间。其通常由产生候选解的方式和候选解产生的概率分布组成。候选解一般按照某一概率密度函数对解空间进行随机采样获得,而概率分布可以为均匀分布、正态分布、指数分布等。
状态转移概率是指从一个状态转换成另一个状态的概率,模拟退火算法中一般采用Metropolis准则,具体如下:
$$f(x)=\left\lbrace\begin{array}{cll}
1 & , & E(x_{new}) < E(x_{old}) \\
exp(-\frac{E(x_{new})-E(x_{old})}{T}) & , & E(x_{new}) \ge E(x_{old})
\end{array}\right.$$
其与当前温度参数T有关,随温度的下降而减小。
冷却进度表是指从某一高温状态T向低温状态冷却时的降温函数,设时刻的温度为T(t),则经典模拟退火算法的降温方式为:
$$T(t)=\frac{T_{0}}{lg(1+t)}$$
而快速模拟退火算法的降温方式为:
$$T(t)=\frac{T_{0}}{1+t}$$
其他方法不再赘述。
一般来说,初始温度越大,获得高质量解的几率越大,但是花费的时间也会随之增加,因此,初温的确定应该同时考虑计算效率与优化质量,常用的方法包括:
1.均匀抽样一组状态,以各状态目标值的方差为初温。
2.随机产生一组状态,确定两两状态间的最大目标值差,然后根据差值,利用一定的函数确定初温,如: $T_{0}=-\frac{\Delta_{max}}{Pr}$ ,其中Pr为初始接受概率。
3.根据经验公式给出。
内循环(求解循环)终止准则:
外循环(降温循环)终止准则:
实例函数: $f(x)=(x^{2}-5x)sin(x^2)$
1 | import numpy as np |
Reference
https://www.imooc.com/article/30160
https://baike.baidu.com/item/模拟退火算法/355508?fr=aladdin
https://blog.csdn.net/google19890102/article/details/45395257
https://www.cnblogs.com/xxhbdk/p/9192750.html
粒子群算法(Particle swarm optimization,PSO)是模拟群体智能所建立起来的一种优化算法,主要用于解决最优化问题(optimization problems)。1995年由 Eberhart和Kennedy 提出,是基于对鸟群觅食行为的研究和模拟而来的。
假设一群鸟在觅食,在觅食范围内,只在一个地方有食物,所有鸟儿都看不到食物(即不知道食物的具体位置。当然不知道了,知道了就不用觅食了),但是能闻到食物的味道(即能知道食物距离自己是远是近。鸟的嗅觉是很灵敏的)。
假设鸟与鸟之间能共享信息(即互相知道每个鸟离食物多远。这个是人工假定,实际上鸟们肯定不会也不愿意),那么最好的策略就是结合自己离食物最近的位置和鸟群中其他鸟距离食物最近的位置这2个因素综合考虑找到最好的搜索位置。
粒子群算法与《遗传算法》等进化算法有很多相似之处。也需要初始化种群,计算适应度值,通过进化进行迭代等。但是与遗传算法不同,它没有交叉,变异等进化操作。与遗传算法比较,PSO的优势在于很容易编码,需要调整的参数也很少。
PSO有几个核心概念:
加速度更新公式:
$$v[i] = w * v[i] + c1 * rand() *(pbest[i] - present[i]) + c2 * rand() * (gbest - present[i])$$
其中v[i]代表第i个粒子的速度,w代表惯性权值,c1和c2表示学习参数,rand()表示在0-1之间的随机数,pbest[i]代表第i个粒子搜索到的最优值,gbest代表整个集群搜索到的最优值,present[i]代表第i个粒子的当前位置。
位置更新公式:
$$present[i]=present[i]+v[i]$$
1.粒子数:粒子数的选取一般在20个到40个之间,但是需要具体问题具体对待,如果对于复杂问题,则需要设置更多的粒子,粒子数量越多,其搜索范围就越大。
2.惯性因子 $w$ :用来控制继承多少粒子当前的速度的,越大则对于当前速度的继承程度越小,越小则对于当前速度的继承程度越大。有些同学可能会产生疑问,是不是说反了。其实不是,从公式中可以明确看出,其值越大,则速度的改变幅度就越大,则对于粒子的当前速度继承越小;反之,速度的改变幅度越小,则对于粒子当前速度继承越大。因此如果的值越大,则解的搜索范围越大,可以提高算法的全局搜索能力,但也损失了局部搜索能力,有可能错失最优解;反之如果的值越小,则解的搜索范围也就越小,算法的全局搜索能力也就越小,容易陷入局部最优。如果是变量,则其值应该随着迭代次数的增加而减小(类似于梯度下降当中的学习率)。如果为定值,则建议在0.6到0.75之间进行选取。
3.加速常数 $c1,c2$ :通过公式一可以看出,加速常数控制着飞翔速度的计算是更加看重自身经验还是群体经验。公式一中的第二项就是自身经验的体现,加速常数可以看做是用来调整自身经验在计算粒子飞翔速度上的权重。同理是用来控制群体经验在计算粒子飞翔速度过程中的权重的。如果为0,则自身经验对于速度的计算不起作用,如果为0,则群体经验对于粒子飞翔速度的计算不起作用。的取值在学术界分歧很大主要有如下几种情况:
| 学者 | 参数取值 |
|---|---|
| Clerc | c1=c2=2.05 |
| Carlisle | c1=2.8, c2=1.3 |
| Trelea | w=0.6, c1=c2=1.7 |
| Eberhart | w=0.729, c1=c2=1.494 |
1 | # -*- coding: utf-8 -*- |
Reference:
https://blog.csdn.net/zhaozx19950803/article/details/79854466
https://blog.csdn.net/yy2050645/article/details/80740641
https://blog.csdn.net/zj15527620802/article/details/81366105
英文: Quality of Service
中文: 服务质量
介绍: 指一个网络能够利用各种基础技术,为指定的网络通信提供更好的服务能力,是网络的一种安全机制,是用来解决网络延迟和阻塞等问题的一种技术。 通过配置QoS,对企业的网络流量进行调控,避免并管理网络拥塞,减少报文的丢失率,同时也可以为企业用户提供专用带宽或者为不同的业务(语音、视频、数据等)提供差分服务。
在正常情况下,如果网络只用于特定的无时间限制的应用系统,并不需要QoS,比如Web应用,或E-mail设置等。但是对关键应用和多媒体应用就十分必要。当网络过载或拥塞时,==QoS能确保重要业务量不受延迟或丢弃==,同时保证网络的高效运行。在RFC 3644上有对QoS的说明。
是当用户需要时网络即能工作的时间百分比。可用性主要是设备可靠性和网络存活性相结合的结果。对它起作用的还有一些其他因素,包括软件稳定性以及网络演进或升级时不中断服务的能力。 在连续5min内,如果一个IP网络所提供的丢包率<=75%,则认为该时间段是可用的,否则是不可用的。
网络带宽是指在单位时间(一般指的是1秒钟)内能传输的数据量。对IP网而言可以从帧中继网借用一些概念。根据应用和服务类型,服务水平协议(SLA)可以规定承诺信息速率(CIR)、突发信息速率(BIR)和最大突发信号长度。承诺信息速率是应该予以严格保证的,对突发信息速率可以有所限定,以在容纳预定长度突发信号的同时容纳从话音到视像以及一般数据的各种服务。一般讲,吞吐量越大越好。
指一项服务从网络入口到出口的平均经过时间。许多服务,特别是话音和视像等实时服务都是高度不能容忍时延的。当时延超过200-250毫秒时,交互式会话是非常麻烦的。为了提供高质量话音和会议电视,网络设备必须能保证低的时延。
产生时延的因素很多,包括分组时延、排队时延、交换时延和传播时延。传播时延是信息通过铜线、光纤或无线链路所需的时间,它是光速的函数。在任何系统中,包括同步数字系列(SDH)、异步传输模式(ATM)和弹性分组环路(RPR),传播时延总是存在的。
是指同一业务流中不同分组所呈现的时延不同。高频率的时延变化称作抖动,而低频率的时延变化称作漂移。抖动主要是由于业务流中相继分组的排队等候时间不同引起的,是对服务质量影响最大的一个问题。
某些业务类型(特别是语音和视频等实时业务)是极其不能容忍抖动的。报文到达时间的差异将在语音或视频中造成断续;另外,抖动也会影响一些网络协议的处理,有些协议是按固定的时间间隔发送交互性报文,抖动过大就会导致协议震荡,而实际上所有传输系统都有抖动,但只要抖动在规定容差之内就不会影响服务质量,另外,可利用缓存来克服过量的抖动,但这将会增加时延。
漂移是任何同步传输系统都有的一个问题。在SDH系统中是通过严格的全网分级定时来克服漂移的。在异步系统中,漂移一般不是问题。漂移会造成基群失帧,使服务质量的要求不能满足。
不管是比特丢失还是分组丢失,对分组数据业务的影响比对实时业务的影响都大。在通话期间,丢失一个比特或一个分组的信息往往用户注意不到。在视像广播期间,这在屏幕上可能造成瞬间的波形干扰,然后视像很快恢复如初。即便是用传输控制协议(TCP)传送数据也能处理丢失,因为传输控制协议允许丢失的信息重发。事实上,一种叫做随机早丢(RED)的拥塞控制机制在故意丢失分组,其目的是在流量达到设定门限时抑制TCP传输速率,减少拥塞,同时还使TCP流失去同步,以防止因速率窗口的闭合引起吞吐量摆动。但分组丢失多了,会影响传输质量。所以,要保持统计数字,当超过预定门限时就向网络管理人员告警。
丢包(packetloss)可能在所有环节中发生,例如:
References:
https://blog.csdn.net/qq_25077833/article/details/53428655
https://blog.csdn.net/kakingka/article/details/45698709
https://blog.csdn.net/qq_38265137/article/details/80466737
本文主要参考官方文档https://lxml.de/tutorial.html整理,如有错误欢迎指出。
1 | from lxml import etree |
1 | # 添加Element默认添加为根节点 |
b'<root><child1/><child2/><child3/></root>'
b'<root>\n <child1/>\n <child2/>\n <child3/>\n</root>\n'
b"<?xml version='1.0' encoding='iso-8859-1'?>\n<root><child1/><child2/><child3/></root>"
<root>
<child1/>
<child2/>
<child3/>
</root>1 | # 每个元素都是一个list |
child1 3
child01 | # 可以用list函数取出子元素的list |
<Element root at 0x107b03888>
[<Element child0 at 0x107b034c8>, <Element child1 at 0x107b03448>, <Element child2 at 0x107b038c8>, <Element child3 at 0x107b03908>]1 | # 通过长度检查element是否为叶子节点 |
root has children
child1 has no child1 | # 不同于普通list,赋值可能会造成元素移动 |
b'<root><child0/><child1/><child2/><child3/></root>'
b'<root><child3/><child1/><child2/></root>'
[0, 1, 2, 3]
[3, 1, 2, 3]1 | # 要拷贝节点,需要调用deepcopy |
b'<root><child3/><child1/><child2/></root>'
b'<newroot><child1/></newroot>'1 | # etree元素自带方法可以找到对应的父节点、前一个节点、后一个节点 |
True
True
True1 | # 属性以字典方式存储 |
b'<root interesting="totally"/>'
totally
None
b'<root interesting="totally" hello="Huhu"/>'1 | # 字典的相关方法也可以直接使用 |
[('interesting', 'totally'), ('hello', 'Huhu')] ['interesting', 'hello'] ['totally', 'Huhu']
None
Guten Tag
Guten Tag
dict_items([('interesting', 'totally'), ('hello', 'Guten Tag')])1 | # 元素中包含文本 |
Hello World
b'<root>Hello World</root>'1 | # 如何添加特殊元素类似于<br/> |
b'<html><body>TEXT</body></html>'
b'<html><body>TEXT<br/></body></html>'
b'<html><body>TEXT<br/>TAIL</body></html>'
b'<html><body>HEAD<br/>TAIL</body></html>'1 | # tail其实属于前边元素的一部分 |
b'<br/>TAIL'
b'<br/>'
b'HEADTAIL'1 | # xpath方法也可以使用 |
HEADTAIL
['HEAD', 'TAIL']1 | # 甚至可以吧xpath的方法包装成函数 |
['HEAD', 'TAIL']1 | # text也可以找爸爸 |
HEAD
body
TAIL
br1 | # 判断一段文本是正常的文本还是tail |
True
False
True1 | # 但是XPath下有些方法就不行了 |
HEADTAIL
None1 | # etree中的树是iterable的 |
b'<root>\n <child>Child 1</child>\n <child>Child 2</child>\n <another>Child 3</another>\n</root>\n'
root - None
child - Child 1
child - Child 2
another - Child 31 | # 可以通过在iter中添加参数,来过滤输出的tag |
child - Child 1
child - Child 2
child - Child 1
child - Child 2
another - Child 31 | # 默认情况下,所有节点都会被遍历,如Entity、Comment等,通过添加tag参数可以避免这一点 |
b'<root><child>Child 1</child><child>Child 2</child><another>Child 3</another>ê<!--some comment--></root>'
root - None
child - Child 1
child - Child 2
another - Child 3
SPECIAL: ê - ê
SPECIAL: <!--some comment--> - some comment
root - None
child - Child 1
child - Child 2
another - Child 3
ê1 | # 通过elementTreeName.write(filePath)可以把树写进文件或通过url传输 |
1 | # 简单粗暴的直接写xml也可以 |
b'<html><head/><body><p>Hello<br/>World</p></body></html>'
b'<html><head></head><body><p>Hello<br>World</p></body></html>'
b'HelloWorld'1 | # ElementTree class,是一个element的容器,提供了一些方法来对整个root node文档进行操作 |
1.0
<!DOCTYPE root SYSTEM "test">
<!DOCTYPE root PUBLIC "-//W3C//DTD XHTML 1.0 Transitional//EN" "file://local.dtd">1 | print(etree.tostring(tree)) |
b'<!DOCTYPE root PUBLIC "-//W3C//DTD XHTML 1.0 Transitional//EN" "file://local.dtd" [\n<!ENTITY tasty "parsnips">\n]>\n<root>\n <a>parsnips</a>\n</root>'
b'<root>\n <a>parsnips</a>\n</root>'1 | # 解析文档中以string读入的xml |
b'<root>data</root>'1 | # 二进制读取解析 |
b'<root>data</root>'
b'<root>data</root>'
root执行: root1 | # parser对象 |
b'<root><a/><b> </b></root>'1 | # Incremental parsing增量解析,比如在网络分步传输的场景下需要使用 |
b'<root>data</root>'
b'<root><a/></root>'1 | # Event-driven parsing事件驱动的解析,如只需要很大的树中的一小部分时使用 |
end, a, data
end, root, None
start, root, None
start, a, data
end, a, data
end, root, None1 | # 方法二 |
1
event: start - tag: root
* test = true
/Users/imonce/anaconda/lib/python3.6/site-packages/ipykernel_launcher.py:15: DeprecationWarning: inspect.getargspec() is deprecated, use inspect.signature() or inspect.getfullargspec()
from ipykernel import kernelapp as app1 | events = etree.fromstring('<root test="true"/>', parser) |
2
31 | for event in events: |
event: start - tag: root
* test = true1 | # namespace命名空间,格式为:{namespace_name}tag_name |
b'<ns0:testhtml xmlns:ns0="http://www.w3.org/1999/test"><ns0:tbody>Hello World</ns0:tbody></ns0:testhtml>'
b'<html:html xmlns:html="http://www.w3.org/1999/xhtml"><html:body>Hello World</html:body></html:html>'1 | # 设置默认命名空间 |
b'<html xmlns="http://www.w3.org/1999/xhtml"><body>Hello World</body></html>'1 | # QName方法,快速合成或提取namespace |
html
http://www.w3.org/1999/xhtml
{http://www.w3.org/1999/xhtml}html
html1 | # nsmap方法,直接提取命名空间字典 |
{None: 'http://www.w3.org/1999/xhtml'}1 | # 子元素继承父元素命名空间 |
{'a': 'http://a.b/c'}
{'b': 'http://b.c/d', 'a': 'http://a.b/c'}1 | # 添加带命名空间的属性,格式为:set({namespace_name}attr_name, attr_value) |
b'<html xmlns="http://www.w3.org/1999/xhtml"><body xmlns:html="http://www.w3.org/1999/xhtml" html:bgcolor="#CCFFAA">Hello World</body></html>'
None
#CCFFAA1 | # 也可以用XPath |
{http://www.w3.org/1999/xhtml}body1 | # iter的话也要考虑namespace |
{http://www.w3.org/1999/xhtml}body1 | # E-factory:提供一种简单紧凑的语法来生成XML和HTML |
<html>
<head>
<title>This is a sample document</title>
</head>
<body>
<h1 class="title">Hello!</h1>
<p>This is a paragraph with <b>bold</b> text in it!</p>
<p>This is another paragraph, with a
<a href="http://www.python.org">link</a>.</p>
<p>Here are some reserved characters: <spam&egg>.</p>
<p>And finally an embedded XHTML fragment.</p>
</body>
</html>1 | # 此外还有一种基于属性的方法 |
<p:doc xmlns:p="http://my.de/fault/namespace">
<p:title>The dog and the hog</p:title>
<p:section>
<p:title tType="title">The dog</p:title>
<p:par>Once upon a time, ...</p:par>
<p:par>And then ...</p:par>
</p:section>
<p:section>
<p:title>The hog</p:title>
<p:par>Sooner or later ...</p:par>
</p:section>
</p:doc>1 | # XPath的一些例子 |
None
a1 | # 找孩子(所有子节点) |
b1 | # 带属性找孩子 |
a1 | # 通过ElementTree找路径 |
a/b[1]
a/c
a/b[2]